Brouwer's fixed point theorem is neat, easy to state and can be used to prove the existence of the Nash mixed equilibrium. It's pretty straightforward to prove on a Euclidean plane with the fundamental group. Higher dimensions call for higher order homotopy groups, but we might just as well use any homology functor. Original proof by Brouwer apparently was done with degrees of maps, but one with homology groups is in my opinion simpler. It also shows a fairly canonical way of using homology in the wild!
BFPT. Let $f: B^n \rightarrow B^n$ be a continuous map. Then there is an $x\in B^n$ such that $f(x)=x$. Here we denote $B^n$ to be a closed ball $\R^n$ and $S^{n-1}$ is its boundary, a sphere in $\R^n$. In fact, any convex bounded subspace works.
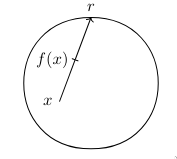
Proof. Suppose otherwise. Cast a ray from $f(x)$ through $x$ to boundary and denote it $r: B^n \to S^{n-1}$. We can prove it is continuous. It is clear that $r$ is identity on boundary. Define $i$ as inclusion map of the boundary, that is, an extension of identity to the ball. Clearly, $r\circ i$ will be remain identity on boundary.
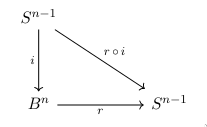
We can draw a new diagram with induced maps and the homology groups. By, say, simplical triangulations or tricks in different homology theories, we also know that for any $n$ the $H_{n-1}(S^{n-1})\cong\Z$ and $H_{n-1}(B^n)\cong 0$.
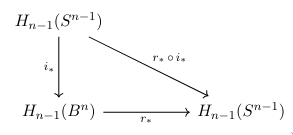
In particular, by the functorial properties of the homology, we have that for induced maps, the $r_*\circ i_*$ must remain identity, now on $\Z$. Let $n$ in $\Z$, then $n=r_*(i_*(n))=r_*(0)=0$. We have a contradiction, but inclusion map exists by construction, so $r$ must not. We conclude there must be a fixed point. $\square$
02 January, 2021