This post notes on a, somewhat abstract, construction of inverse limits on groups. These are certain well-behaved subsets of similarly-well-behaved families of algebraic objects (like groups). Many fiddly structures can be easily constructed as inverse limits, and many nice properties of the building blocks used for the inverse system continue to hold for the limit object. We focus on groups for simplicity, but this works for many other structures (compact groups, topological spaces, what-have-you). There is a powerful application to algebraic topology: the construction of Cech homology. It's one of the first generalizations of simplicial homology; it strays a bit from Eilenberg-Steenrod axioms (exactness breaks), but it has stronger properties of continuity w.r.t. inverse systems, which make it useful in e.g. fancy game theory.
Definition. Directed sets. Start with a transitive and reflexive relation $<$ on some set $I$ and require that for all $i,j\in I$ there is $k\in I$ with $i,j<k$. A subset $J\subset I$ is said to be cofinal in $I$ if for every $i\in I$ there is $j\in J$ with $i<j$.
Definition. Inverse system. Let ${X_i}$ be a collection of groups indexed by a directed set $I$. For $i<j$ let $\pi^{j\to i}\colon X_j\to X_i$ be a homomorphism such that $\pi^{i\to i}$ is identity and if $i<j<k$ then $\pi^{j\to i}\circ \pi^{k\to j}=\pi^{k\to i}$. We usually suppress notation to $(X,\pi)$ and specify the directed set. Also works for things with "more structure" such as topological spaces or continuous groups e.g. $SO(3)$.
Definition. Inverse map. Let $(X, \pi)$ and $(Y, \tau)$ be inverse systems over $I$ and $J$ respectively. Define $\Phi\colon (X,\pi)\to (Y,\tau)$ to consist of a set map $\varphi\colon J\to I$ and a collection of group homomorphisms $\varphi_{j}\colon X_{\varphi(j)}\to Y_{j}$ for all $j\in J$ such that if $k>j$ in $J$. We can prove that following diagram commutes
\begin{CD} X_{\varphi(k)} @> \pi^{\varphi(k)\to\varphi(j)} >> X_{\varphi(j)} \\ @VV\varphi_kV @VV\varphi_jV \\ Y_k @> \tau^{k\to j} >> Y_j \end{CD}
Definition. Inverse limits. Let $(X_i, \pi^{j\to i})_{i< j}$ be an inverse system over $I$. Let $\Pi_{i\in I} X_i$ denote the infinite Cartesian product of groups $X_i$. The inverse limit of $(X,\pi)$ is defined as
$$X_\infty=\{x\in \displaystyle\Pi_{i\in I}X_i\mid x_i=\pi^{j\to i}(x_j) \:\forall i<j\}$$
We can prove this set is non-empty and also forms a group. Informally, an element of the inverse limit is a sequence of "valid choices" of elements of $X_i$.
For example, consider finite sets $X_i$ indexed by $i\in\N$ such that $|X_i|=2^{i-1}$. Let $\pi^{j\to i}$ be such that it maps two unique elements from $X_j$ to one unique element in $X_i$. This forms an inverse system. If we interpret it as an infinite complete binary tree, its limit is the set of all infinite paths starting at the singleton $X_1$. In the picture below, the path, or the "thread" of choices, is valid because it does not "jump" to "illegal" subsets. In fact, with the subspace topology, this construction results in the Cantor set!
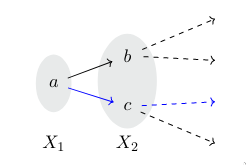
We can also "recover" a particular choice of an element of $X_i$. Define the projection $\pi_i\colon X_\infty\to X_i$ by $\pi_i(x)=x_i$ such that if $i<j$ then $\pi_i=\pi^{j\to i}\circ\pi_j$. One can prove this exists and is a group homomorphism.
Lemma. If component homomorphisms are isomorphic, then so is the projection. Let $(X, \pi)$ be an inverse system over $I$. Suppose for each $i,j\in I$ such that $i<j$ the $\pi^{j\to i}\colon X_j\to X_i$ is an isomorphism. Then for each $i\in I$ the projection $\pi_i \colon X_\infty\to X_i$ is an isomorphism.
Now, we would like to relate the limits of systems related by an inverse map.
Definition. Limit maps. Let $\Phi\colon (X,\pi)_I\to (Y, \tau)_J$ be an inverse map. There is a $\varphi_\infty\colon X_\infty\to Y_\infty$ such that
\begin{CD} X_{\infty} @> \pi_{\varphi(j)} >> X_{\varphi(j)} \\ @VVV @VVV \\ Y_\infty @> \tau_j >> Y_j \end{CD}
Lemma. Limit maps of cofinal systems are isomorphic. Let $(X, \pi)$ and $(X', \pi')$ be inverse systems over $I$ and $C$ respectively. Let $C$ be cofinal in $I$. Let $\Phi\colon (X,\pi)\to (X',\pi')$ be an inverse map. Let $\varphi_\infty\colon X_\infty\to X'_\infty$ be its limit. Then $\varphi_\infty$ is an isomorphism.
Next, I think I'll write up how this fits in with simplicial homology. There is a nice proof of the fact that on finite polytopes, Cech and simplicial homology groups coincide. This easily leads to topological invariance of simplicial homology, a result that is (in my opinion) a bit trickier to prove using the more classical way of simplicial maps. Of course, simplicial maps are still preferable since they work on infinite polytopes, but oh well hehe.
10 April, 2021